This post describes what I call “CTP Theory”, which is my attempt at a theory of AGI, or Artificial General Intelligence. I have written before about CTP Theory, but there have been some significant changes in the theory, and in the way that I think about it, so much of my old writing on the subject is outdated. The purpose of this post is to provide an updated overview of the theory, and the problems with it that I’m currently thinking about.

No knowledge of my prior writings about CTP Theory is necessary to understand this post, though I do assume a general familiarity with Critical Rationalism, the school of epistemology developed by Karl Popper. I’ve avoided using technical language as much as possible, though some familiarity with programming or mathematics may be helpful. I will provide technical details in the endnotes where I feel it is necessary.

An Epistemological approach to AGI

An AGI is a computer program capable of performing any mental task that a human being can. In other words, an AGI needs to be just as good as a human at gaining knowledge about the world. There has been a long history of discussion in the field of epistemology on the topic of how exactly humans manage to be so good at gaining knowledge. Having a good understanding of how humans gain knowledge, which is to say a good theory of epistemology, is essential for solving the problem of creating an AGI.

The best theory of epistemology that anyone has managed to come up with yet is, in my opinion, Critical Rationalism (CR), which was originally laid out by Karl Popper. The details of CR are not the focus of this article, but it is important to note that many proposed approaches to AGI are incompatible with CR, which means that, if CR is correct, then those approaches are dead ends.

Any theory of how to create an AGI is, at least implicitly, a theory of epistemology: a theory about what kinds of systems can create knowledge, and how. Similarly, many theories of epistemology can be thought of as partial theories of AGI, in the sense that they describe how an AGI must work in order to be able to create knowledge. Developing a theory of AGI is thus, in a sense, equivalent to developing a theory of epistemology that is sufficiently detailed to be translated into computer code. CTP Theory is my attempt to come up with such a theory by elaborating on Critical Rationalism.

Contradictions

In the essay “What is Dialectic?” (which appears in his book Conjectures and Refutations), Popper says that “criticism invariably consists in pointing out some contradiction”. I think that this is one of the most important ideas in Critical Rationalism, and it provides a valuable guideline for theories of AGI: Any Popperian theory of AGI must recognize contradiction as the basis for criticism, and must include a detailed account of how the mind manages to find, recognize, and deal with contradictions. This has been one of my primary goals in trying to develop a Critical Rationalist theory of AGI, and I think that CTP Theory provides a satisfying account of how the mind can manage to do these things.

Let us start with the question of how a mind can find a contradiction between two ideas. To illustrate this problem I’ll return to an example I used in my first post on CTP Theory : consider the statements “My cat is calico”, and “My cat is male”. We can see (assuming the reader is familiar with the fact that only female cats can be calico) that these statements are contradictory, but how is it that we can see that? There are some pairs of statements, such as “my cat is female” and “my cat is not female” which are quite obviously contradictory, and we can call these kinds of pairs of statements “directly contradictory”. The statements “My cat is calico” and “My cat is male” aren’t directly contradictory, but they still seem to be contradictory in some way.

CTP Theory’s explanation of how the mind detects such indirect contradictions begins by assuming that the mind has a built-in ability to detect direct contradictions. In other words, we start with the assumption that the mind can perform the trivial task of identifying that two statements like “My cat is female” and “My cat is not female”, or more generally “X is true” and “X is false”, are contradictory [1]. This assumption turns out to allow us a way to detect indirect contradictions, as well: Two (or more) ideas are indirectly contradictory if they imply a direct contradiction.

The statements “My cat is calico” and “My cat is male” are indirectly contradictory, because though they are not themselves directly contradictory, they imply a direct contradiction. “My cat is calico” implies “My cat is female”, and “My cat is male” implies “My cat is not female”. “My cat is female” and “My cat is not female” are directly contradictory, so the mind knows that the statements “My cat is calico” and “My cat is male” imply a direct contradiction despite not being directly contradictory themselves.

Implications

We’ve shown that if the mind has a built-in way to detect direct contradictions, it can also detect indirect contradictions by searching through the relevant ideas’ implications and finding a direct contradiction. But how does the mind know what the implications of an idea are?

In the example I gave, I said that the statement “My cat is calico” implies the statement “My cat is female”, but that is somewhat of a simplification. To be more precise, “My cat is female” is an implication not only of the idea “My cat is calico”, but also of the idea “All calico cats are female”. Both of those ideas are necessary to derive the idea “My cat is female”, neither alone is enough. Similarly, I said “My cat is not female” is an implication of “My cat is male”, but to be more precise it is an implication of “My cat is male” along with “A cat that is male is not female”.

How can the mind know exactly what the implications of two (or more) given ideas are, if there are any? For instance, how would the mind derive “My cat is female” from the “My cat is calico” and “All calico cats are female”? CTP Theory answers that question by saying that some ideas are functions, in the mathematical sense of the term. Specifically, ideas are functions that take some number of other ideas as inputs, and return an idea as an output [2]. In other words, some ideas can produce new ideas based on the content of other ideas. By thinking of ideas as functions, we have a rigorous way of defining what the implications, or logical consequences, of an idea are: whenever an idea is invoked as a function with some set of other ideas as inputs, the resulting idea is a consequence of the idea being invoked and the ideas used as inputs [3].

As I said before, the statements “My cat is calico” and “All calico cats are female” taken together imply the statement “My cat is female”. In this case, we can think of the statement “All calico cats are female” as a function, and “My cat is calico” as an input being supplied to that function. Specifically, the statement “All calico cats are female” can be thought of as a function that takes in a statement that some cat is calico, and returns a statement that the same cat is female. Just as it takes in the statement “My cat is calico” and returns “My cat is female”, it could also take in the statement “Jake’s cat is calico” and return the statement “Jake’s cat is female”. For statements that don’t state that some cat is calico, the function would return no output, or in other words it would be undefined for that input. It would not return any new ideas if a statement like “My cat is sleeping” or “My cat is brown” or “The sky is blue” were provided to it, as the function is not defined for those inputs.

Tracing a Problem’s Lineage

So we have an explanation for how the mind finds the implications of its ideas and finds contradictions between them, but what should the mind do when it finds a contradiction? When two or more ideas contradict, at least one of them must be wrong, so the mind can use a contradiction as an opportunity to potentially correct an error. The first step in doing that is identifying the set of ideas that are involved in the contradiction.

The two ideas that directly contradict in our example are “My cat is female” and “My cat is not female”, but the contradiction cannot be fully understood in terms of those two ideas alone. These two statements are the logical consequences of other ideas, and so we need to work backwards from the two directly contradictory ideas to the set of all ideas which are logically involved in the contradiction. In other words, we need to be able to identify the set of indirectly contradictory ideas that resulted in a particular direct contradiction.

Let’s look at a diagram that lays out all of the ideas I’ve used so far, as well as a few others:

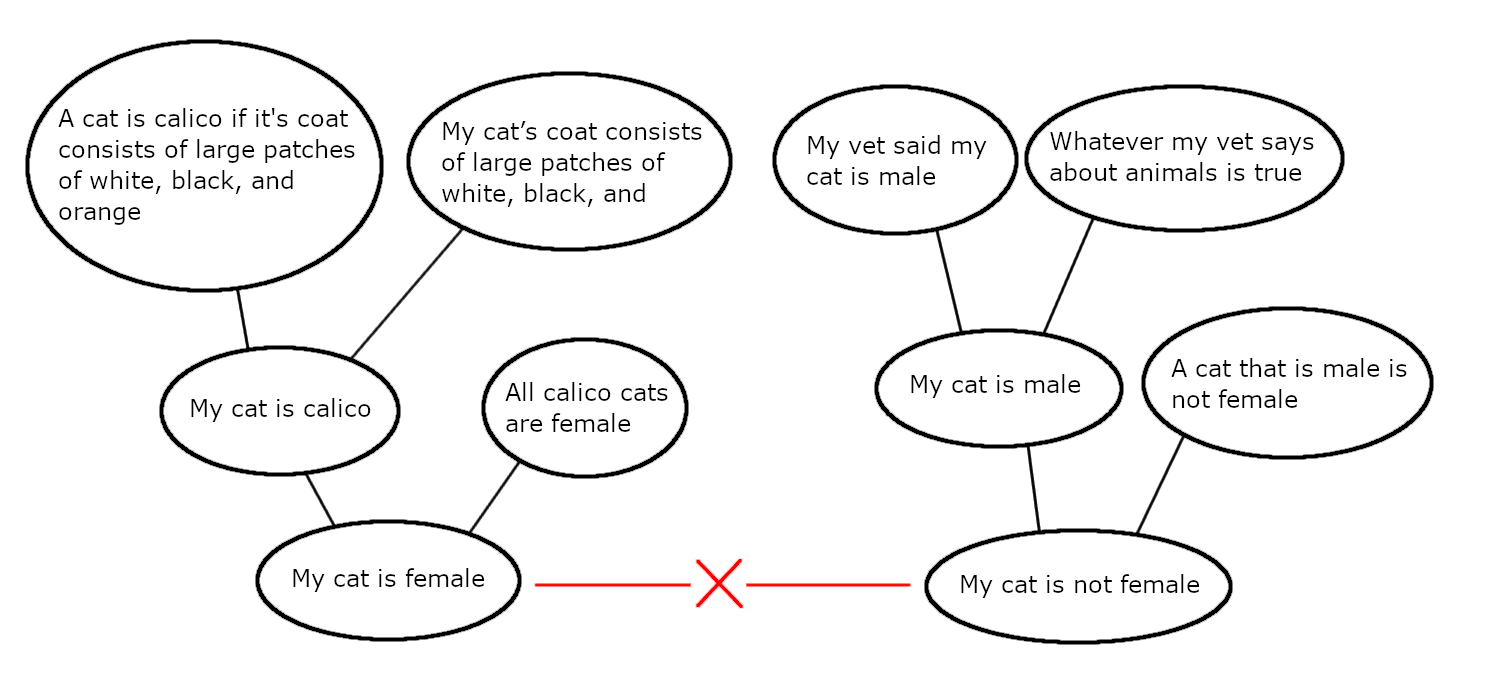
This diagram lays out the relationships between all of the ideas we’ve used so far, along with a few new ones: “My cat is male” was derived as the consequence of two other ideas “My vet said my cat is male” and “Whatever my vet says about animals is true”, and “My cat is calico” was derived as the consequence of the ideas “A cat is calico if it’s coat consists of large patches of white, black and orange” and “My cat’s coat consists of large patches of white, black, and orange”.

In logic, if some idea P implies and idea Q, then P is referred to as the “antecedent” of Q. In this diagram, ideas are displayed below their antecedents, with lines showing exactly which ideas are implications of other ideas. Some of the ideas in the diagram, such as “My cat’s coat consists of large patches of white, black, and orange” and “A cat that is male is not female”, have no antecedents on the diagram. In CTP Theory, ideas which have no antecedents are called “primary ideas”, and ideas which do have antecedents, i.e. ideas which are the consequences of other ideas, are called “consequent ideas” or “consequences”.

Primary ideas, rather than being derived from any other ideas, are created through conjecture, a process in which the mind blindly varies existing ideas to produce new ones. All conjectures, according to CTP Theory, take the form of primary ideas.

While consequent ideas are not directly created by conjecture, it is important to understand that they still have the same epistemic status as primary ideas. CR says that no idea is ever justified, and no idea ever moves beyond the stage of being conjectural, and any idea can be overturned by some unexpected new idea that effectively critiques and/or replaces it. All of that is true for consequent ideas just as much as primary ideas. Though consequent ideas are not created through conjecture in the same sense that primary ideas are, the are still the consequences of primary ideas, which is to say that they are the consequences of blind conjectures, and as such they should not be thought of as any less conjectural or uncertain as primary ideas.

The ideas in the diagram above that don’t have any lines pointing to them, and thus thus appear to be primary ideas, are not necessarily representative of what primary ideas in a real mind would look like. For instance, the idea “My cat’s coat consists of large patches of white, black, and orange” would almost certainly not be a primary idea, but instead would be a consequence of ideas that are about how to interpret sensory data. I am merely declaring that they are primary ideas for the sake of this demonstration, and I do not intend to imply that they are realistic depictions of what primary ideas would look like in a real mind.

In a situation where we have two directly contradictory consequent ideas, we want to know the set of all ideas involved in the contradiction, which means that we want to know the set of all ancestors to one of the contradictory ideas (by “ancestor” I mean either an antecedent, or an antecedents antecedent, etc.). We can find this if we imagine that each idea in the mind keeps track of what it’s own antecedents are. In other words, if each consequent idea keeps a record of what ideas created it, then the mind can find any idea’s set of ancestors. Any consequent idea will have a record of it’s antecedents, and if any of those antecedents is consequent then it will also have a record of its antecedents, so the mind can continually trace backwards to find all of an idea’s ancestors.

A partial picture of the mind

I imagine that the mind of an AGI working according to CTP Theory, as I’ve described it so far, would basically work like so:

The mind contains a set of ideas, which we can call the mind’s idea-set. When the AGI is started, it’s idea-set will be initialized with some starting set of ideas (perhaps these ideas would need to be decided by the programmer, or perhaps they could simply be created by some algorithm that blindly generates starting ideas). These starting ideas are all primary ideas, since they have no antecedents. After initialization, the mind enters an iterative process of computing the implications of the ideas in the idea-set, and adding those implications, in the form of consequent ideas, to the idea-set. Through this iterative process the mind explores the implications of it’s ideas. The mind checks each new consequent idea it computes against all of existing ideas in the idea-set to see if the new idea directly contradicts any of them. In other words, the mind attempts to criticize it’s ideas by exposing them to one another and seeing where they contradict. Eventually, it might notice two of it’s ideas are directly contradictory, which means that it has a problem. The mind then attempts to solve the problem by modifying the idea-set in a way that resolves the contradiction, and then continues on exploring the implications of it’s ideas (including the implications of any new ideas created as part of the process of solving problem, if there are any).

I’ve explained so far how the mind can deduce the implications of it’s ideas, how the mind can notice problems (i.e. contradictions), and how to find the set of ideas responsible for a problem. But how, given that information, does the mind actually solve a problem?

Solving A Problem

In CTP Theory, a “problem” is seen as a direct contradiction that the mind finds between the ideas within it. A problem is essentially a pair of two directly contradictory two ideas, so “solving” a problem could be thought to mean somehow changing the mind such that there is no longer a contradiction.

For the mind to no longer contain a contradiction, one (or both) of the two directly contradictory ideas involved in the problem ideas must be removed from the idea-set. Consider what would happen if the mind simply picked one of the two directly contradictory ideas, and discarded it from the idea-set. The mind would no longer contain a direct contradiction, so in a technical sense the problem could be said to be “solved”. However, if the idea removed is a consequent idea, then simply removing that idea alone wouldn’t make sense. For instance, if the mind wanted to remove the idea “My cat is female”, it would not make sense to try to discard that idea while hanging onto the ideas “My cat is calico” and “All calico cats are female”, because those ideas imply “My cat is female”. A consequent idea is a logical consequence of its antecedents, so you can’t really get rid of the consequent idea without removing it’s antecedents, or at least some of them. Even if the mind did simply discard a consequent idea from its idea-set, that same idea could just be re-derived later from its antecedents, at which point the same problem would appear again. So simply removing one of the directly contradictory ideas is a fruitless way of attempting to solve a problem.

Consider again the diagram from earlier, with a small modification:

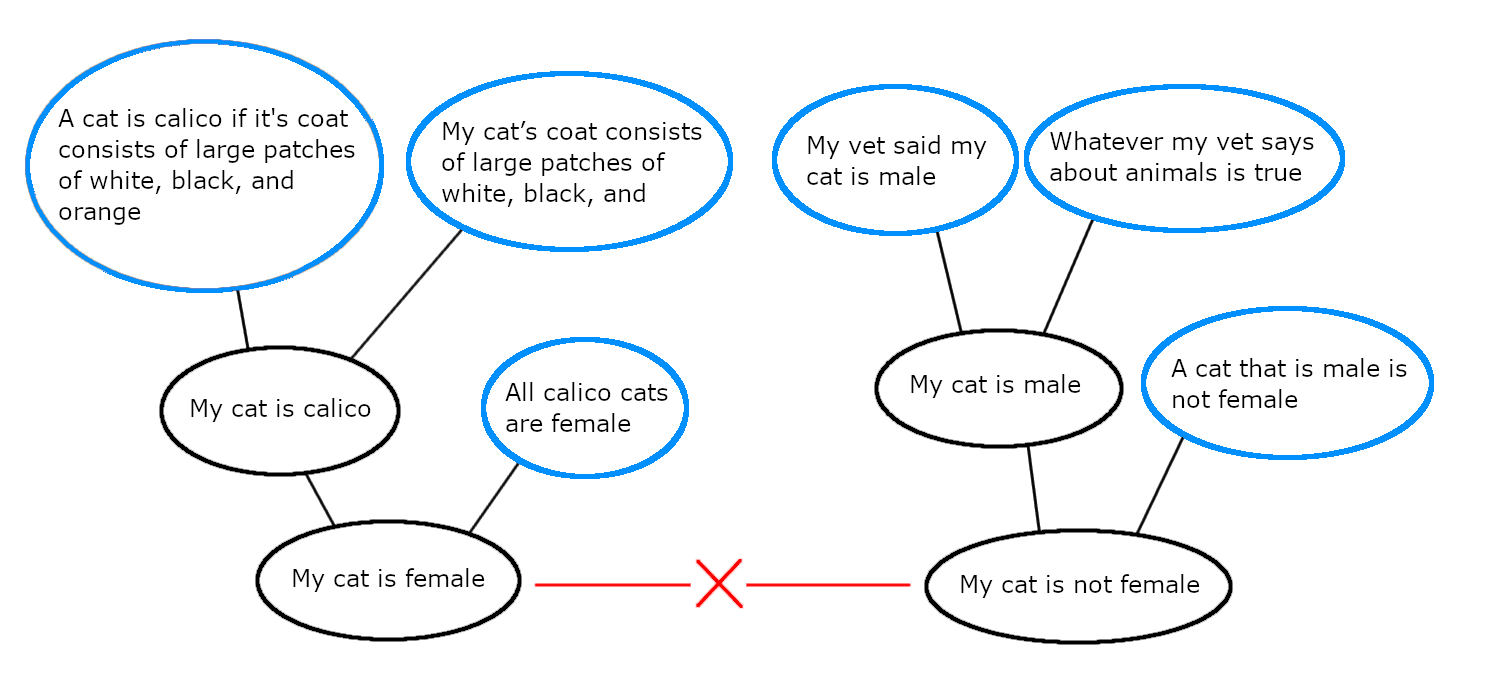
This time, I’ve highlighted the primary ancestors of the directly contradictory ideas “my cat is female” and “my cat is not female” in blue.

Imagine that the mind has decided to solve the contradiction by getting rid of the idea “My cat is female”. As I’ve argued it can’t simply remove that claim alone, because it is a logical consequence of it’s antecedents: “My cat is calico” and “All calico cats are female”. Could the mind solve the problem by removing one of these antecedents, so that “My cat is female” is no longer an implication of any ideas in the mind? It could choose either of the antecedents to remove, but let’s imagine that it chooses the antecedent idea “My cat is calico”. Unfortunately, if the mind tries to solve the problem by removing “My cat is female” and “My cat is calico”, it runs into the same issue I already described, because “My cat is calico” is also a consequent idea. Removing “My cat is calico” without removing its antecedents doesn’t make sense, because it is a logical consequence of its antecedents, and it could be re-derived from them again later.

So removing any consequent idea from the mind without removing one or more of its antecedents never makes sense, because the consequent idea could just be re-derived from the antecedents. Primary ideas, however, are not derived from anything, they are the direct results of blind conjecture. A primary idea removed from the idea-set will stay removed, unless the mind happens to recreate the same idea at some point in the future.

The fact that primary ideas can be freely removed from the idea-set provides an effective way for the mind to resolve contradictions: Find the set of ideas that are ancestors to either of the two contradictory ideas, and then pick out the subset of those ancestors which are primary, not consequent. If the mind removes at least one of those primary ancestors, along with all of its consequences (including it’s “nth-order” consequences, i.e. the consequences of its consequences, and the consequences of consequences of its consequences, etc), then one of the two contradictory ideas will be removed, and the contradiction will not re-emerge [4]. Thus, the ideas ideas highlighted in the above diagram, the set of primary ancestors of the two directly contradictory idea, are the set of ideas that can be removed as a way to solve our example problem.

Constraints on problem-solving

I’ve shown that a mind working according to CTP Theory could solve a problem, i.e. resolve a direct contradiction between two ideas in its idea-set, by removing one or more of one of the directly contradictory ideas’ primary ancestors from the idea-set. However, that can’t be all there is to the mind, because if it was, the behavior of the mind would be trivial. Whenever the mind found a problem, any direct contradiction between two ideas, it could solve the problem by arbitrarily picking a primary ancestor of one of the two ideas, and removing it from the idea-set [5]. If that were all there is to the mind then there would be no need to conjecture, since any problem in the mind could be solved by a simple, mechanical process. Problem-solving obviously isn’t that simple, as it involves creativity and many attempts at conjecture, so clearly CTP Theory, as I’ve described it so far, is missing something important.

In my post “Does CTP Theory Need a new Type of Problem? ” I discussed this issue and proposed a solution for it. The solution I laid out in that article is still the best one that I’m aware of, though the way that I think about the solution has changed somewhat, so I’ll explain the idea again in a way that is more in line with the way that I currently think about it.

One way to think about the problem with CTP Theory is that the mind never has any reason not to discard an idea. A problem is a contradiction between two ideas, and removing an idea from the idea-set will never lead to a new contradiction, so removing an idea never causes any new problem. Since there’s an easy way to solve any given problem by removing some primary idea, and the mind never has any reason not to discard an idea, problem-solving is trivialized. So, if the mind did have some system that gave it a reason not to discard certain ideas, more sophisticated types of problem-solving might be necessary to solve problems. What might a system that gives the mind a reason not to discard an idea look like?

The best answer that I’ve been able to come up with is that the mind contains “requirements” (they could just as easily be called “criteria” or “desires”, as there isn’t any term that perfectly captures the concept I’m trying to express, so I’ll just refer to them as “requirements”). The essential characteristic of a requirement is that it can be fulfilled by a certain kind of idea, and the mind wants all of it’s requirements to be fulfilled. A requirement is essentially something that specifies that the mind wants [6] to have an idea that has certain features. If the mind’s idea-set contains any idea that has the features that a requirement specifies, then that requirement is said to be “fulfilled”, otherwise it is “unfulfilled”.

If there is a requirement that is fulfilled by a single idea in the mind’s idea-set, removing that from the idea-set would lead to the requirement being unfulfilled. Since the mind wants each of its desires to be fulfilled, the mind would have a reason not to remove an idea if it would lead to a requirement being unfulfilled. Thus, this system of requirements can provide a reason for the mind not to discard certain ideas when trying to solve a problem.

An example of the requirement system

In addition to providing a low-level reason not to simply discard ideas when trying to resolve a contradiction, I believe this system of requirements helps explain some higher-level properties of how the mind works in terms of CTP Theory, in a way that I think aligns nicely with ideas in CR. Let us consider an example, to see how this system would work in a real-life situation:

For a long time, many people thought that Newton’s theory of gravity was the correct explanation for why the planets in our solar system behaved as they did. However, in the 19th century, people began to notice that Mercury moved differently than was predicted by Newton’s theory. Now, there was a problem, a contradiction between the predictions of a theory and the results of an experiment. Scientists spent decades trying to solve this problem, and it was finally solved when Albert Einstein introduced his theory of General Relativity, which produced the proper predictions for Mercury’s behavior.

Now let’s consider this scenario in terms of CTP Theory. Consider the scientist who first performed the measurements that contradicted the predictions of Newton’s theory of gravity. That scientist would have had an understanding of Newton’s theory, which means that his mind contained some set of ideas that allowed him to compute the predictions of the theory given some set of initial conditions. With that set of ideas, the scientist might compute an idea like “Right now, mercury is at position X”, where X is some particular position in space. The scientist would also presumably have an understanding of how to use a telescope and whatever other experimental apparatus is involved in measuring the current position of a planet like mercury. In CTP-Theoretic terms, that means that the scientist contains a set of ideas that allows him to interpret his sense-data [7] to compute an idea like “Right now, mercury is at position Y”. When the scientist performed the measurements and calculations necessary to find the values of X and Y, i.e. the predictions of Newton’s theory and the position of Mercury according to his experiment, he would find that they were different, which would mean he has found a contradiction between the ideas in his mind [8].

What would this scientist do after finding this contradiction, according to CTP Theory? If we consider the version of CTP Theory that doesn’t include the requirement system, then the scientist’s behavior would be quite simple: he might merely discard Newton’s theory from his mind (or one of the ideas that is composes it, if the theory is embodied in multiple ideas in the idea-set rather than just one), and proceed on with his day unbothered. We can imagine that, if he went on to tell other scientists about his measurements, they would also simply discard Newton’s theory, and none of them would find it problematic to do so, assuming they are all also acting according to the version of CTP Theory which doesn’t include the requirement system.

Clearly, this wouldn’t be the reasonable way for the scientists to respond. Newton’s theory of gravity is a very powerful theory for making predictions about the universe, and if we were to discard it, there would be many things about the world which we could no longer explain (at least, if we put ourselves in the shoes of someone who lived before Einstein proposed General Relativity). The goal of science, and, in some sense, reason more generally, is to explain things, so throwing out a theory as explanatorily powerful as Newton’s theory without a good replacement is not a reasonable thing to do. However, according to the version of CTP Theory that does not include the requirement system, the scientists’ minds would never have any reason not to discard a theory. The mind’s only motivation would be to avoid contradictions, so if throwing out Newton’s theory would help resolve a contradiction, then the mind would have no issue with doing that.

Adding the requirement system to CTP Theory resolves this issue, and explains why the scientists acted the way they did in reality. When we put ourselves in the shoes of the scientist noticing the discrepancy, we see that there is something wrong with discarding Newton’s theory without any replacement, because we want to be able to explain some of the things that Newtons’ theory explains. We want to be able to understand the motions of the planets, and understand how things move under the influence of gravity on earth. In CTP Theory, each of those things that we want would be a requirement, which Newton’s theory fulfills. It could also be the case that there are smaller, more specific desires, which are indirectly fulfilled by Newton’s theory, in the sense that they are fulfilled by some consequence of Newton’s theory. For instance, a particular scientist might want to know the position of Mars at some moment in time, and she may use Newton’s theory to calculate it. In that case, the scientist’s mind would contain a requirement that can be fulfilled only by a statement like “The current position of Mars is X”. While Newton’s theory wouldn’t directly satisfy that theory, it can be thought of as indirectly fulfilling it, because one of its consequences directly fulfills it. And, since the mind must discard an idea’s consequences whenever it discards an idea, discarding Newton’s theory would lead to that requirement, and any other requirements that Newton’s theory directly or indirectly fulfills, becoming unfulfilled.

So if the mind has any requirements that Newton’s theory directly or indirectly fulfills, then the mind would have a reason not to discard Newton’s theory. However, that is only true for as long as Newton’s theory is the only theory in the mind that fulfills those requirements. If the mind has a requirement that is fulfilled by two (or more) ideas in it’s idea-set, then either of those ideas can be discarded without issue, as discarding one of them will not lead to the requirement becoming unfulfilled, as long as the other is still around to fulfill it. So, if all of the requirements that were fulfilled by Newton’s theory were also fulfilled by some other theory, then Newton’s theory could be freely discarded. And that is in fact exactly what happened when Einstein’s General Relativity came along. General Relativity could explain everything that Newton’s theory had previously been used to explain, but it didn’t make the erroneous prediction Mercury’s orbit that Newton’s theory did. A mind that was aware of both Newton’s Theory and General Relativity would be in quite a different situation than one which only contained Newton’s Theory, because General Relativity would fulfill all of the requirements that Newton’s Theory fulfilled (assuming there had been sufficient time for the mind to sufficiently explore GR’s implications). So now the mind could discard Newton’s Theory without leading to any requirements being unfulfilled, and in doing so it would be able to get rid of the contradiction between Newton’s Theory and the experimental data (or, more precisely, it’s interpretation of the experimental data).

Thus, including the requirement system in CTP Theory allows it to explain why scientists don’t simply solve problems by arbitrarily discarding one of the relevant ideas: An idea can only be discarded once the mind has a good replacement for the idea, which is to say a new idea (or set of new ideas) which satisfies all the requirements that were satisfied by the old idea.

Conjectures

With the addition of the requirement system, CTP Theory can explain not only how the mind finds problems, but also how it decides whether a modification intended to resolve a problem is acceptable: if a modification to the idea-set removes a contradiction without leading to any requirements becoming unfulfilled, then that modification is acceptable. But how can the mind come up with potential changes to the idea-set in the first place?

A core idea in CR is that all new ideas are conjectures, which is to say that they are created by blindly varying and combining the parts of ideas already within the mind. So, CTP Theory must incorporate some method that allows it to create new ideas based on the old ideas in the mind, in whatever form they are represented. Thankfully, there are methods for performing this kind of blind variation that are already well-known within computer science [9].

The problem solving process

When I explained earlier how CTP Theory viewed the mind, I did not lay out exactly how it would go about trying to solve a problem, because I hadn’t described how the requirement system worked yet. Now that I’ve explained the requirement, and how new ideas can be conjectured, I can explain in more detail how a mind would go about trying to solve a problem, according to CTP Theory:

When the mind encountered a problem, a set of two directly contradictory ideas, it would first find the set of all ancestors of the two ideas, as well as the set of their primary ancestors. Then, the mind then would begin to make tentative, conjectural modifications to the idea-set. Each modification could remove any number of ideas from, and add any number of newly conjectured ideas to, the idea-set. The mind then explores the consequences of this modified version of the idea-set, trying to answer two questions:

Does this modification resolve the direct contradiction, i.e. does it prevent at least one of the two directly contradictory ideas not to be derived? Does this modification lead to any requirements becoming unfulfilled? If the answer to the first question turns out to be “Yes”, and the second “No”, then the modification can be accepted. It resolves the problem, while not leaving any requirements unfulfilled. If the answers are anything else, the modification is rejected [10], and the mind restarts this process by generating a new tentative modification.

By iteratively applying this process, the mind can attempt to solve its problems through creative conjecture, just as CR describes [11].

Problems with the requirement system

CTP Theory is still a work in progress (otherwise I’d be creating an AGI rather than writing this article), and the area that needs the most work is, I think, the requirement system. The overarching problem with the requirement system is that it hasn’t been made specific enough. I think that the description I gave of the requirement system, and how it could help explain how the mind’s behavior, is a good start, but it isn’t detailed enough to be translated into computer code. More work is necessary to figure out the details.

Trying to figure out a way to fill in the details of the requirement system is, at the moment, my main priority in developing CTP Theory. So, to conclude this post, I’ll list some of the questions that I’m thinking about relating to the requirement system:

What form do requirements take in the mind? How does the mind determine whether an idea fulfills a requirement? How are requirements created in the mind? Are they somehow computed as the consequences of ideas, or perhaps as consequences of some special kind of idea, or are they created by another system entirely? How can the mind criticize it’s requirements? Can two requirements contradict one another, like normal ideas can, or is there some other kind of system for this purpose?

Endnotes

[1] One apparent problem with this assumption is that it isn’t easy to specify a rule for deciding whether two ideas are directly contradictory when they are expressed in a natural language like English. I used English to express the examples I gave in this post for the sake of simplicity, but of course ideas in the mind would not generally take the form of English sentences. Instead, according to CTP Theory, ideas would take the form of instances of data structures that contain arbitrary data. The mind would also contain a rule for deciding whether two of these data structures are directly contradictory. For instance, the data structure representing ideas could be a bit string of arbitrary length, and two such ideas would be contradictory if and only if they had the same length and shared the same value for all bits but the first. When viewed in this way it is clear that any idea, in isolation, has little, if any, inherent meaning. Instead, ideas take on meaning in the way that they interacted with the other ideas in the mind, i.e. what their implications are and what other ideas they contradict.

[2] Alternatively, functions could be allowed to return any number of ideas as outputs, rather than only a single idea. All of the returned ideas could be considered implications. I don’t yet know whether this change would lead to any significant differences in the algorithm’s capabilities.

[3] Since ideas would be represented as instances of data structures, the mind needs to have some way to interpret these data structures as functions in order for ideas to have implications. To accomplish this, a mind would contain a programming language, which I call the mind’s “theory language”. The theory language and the type of data structure used to represent ideas need to be compatible, in the sense that the language needs to be able to interpret instances of the data structure as code. Depending on the characteristics of the theory language, there may be some possible ideas, or in other words some instances of the right kind of data structure, which don’t form a valid function in the theory language. Ideas of this kind may be used as inputs to other ideas when they are interpreted as functions, but can not be invoked as functions themselves.

[4] It’s possible that a mind could find more than one way to derive an idea, and in this case the process of removing that idea becomes slightly more complex. Imagine that the mind that had two different ways of deriving the idea “My cat is female”: from “My cat is calico” and “All calico cats are female”, or from “My cat gave birth to kittens” and “Only female cats can give birth to kittens”. In that case, the idea “My cat is female” could be said to have two different ancestries, and removing the idea “My cat is female” would require removing one or more primary ideas from each set of ancestors.

[5] This method doesn’t necessarily work if one of the ideas involved in the direct contradiction has been derived by the mind in more than one way. To remove such an idea, you would need to discard at least one primary idea from each of the idea’s lineages.

[6] When I use the term “want” as I do in this sentence, and in the following paragraph, I do not mean that the mind would have a conscious, explicit desire for each one of it’s requirements. Instead I’m using the term in a somewhat metaphorical way, similar to how one might speak of what a gene “wants” when discussing the theory of evolution: the system behaves as one might expect if you imagine that it “wanted” certain things. All that I mean to say is that the mind acts in a way such that it tends to avoid having its desires unfulfilled, and while some requirements might be related to explicit desires, not all will.

[7] In CTP Theory, sense-data is thought to enter the mind in the same format as an idea (described in the first endnote). While mere sense data should not really be thought of as an “idea” or “theory” on an epistemological level, it is convenient for technical reasons to allow sense-data to take the same form as an idea, because it allows sense-data to be used as inputs to ideas being interpreted as functions, in the same way that other ideas can be used. This allows for theory-laden interpretation of sense data, just as CR describes.

[8] While “Right now, mercury is at position X” and “Right now, mercury is at position Y” where X is not equal to Y are not directly contradictory, the scientist’s mind would presumably have some idea that would allow it to derive “Right now, mercury is not anywhere other than position X” from “Right now, mercury is at position X”, and some other idea that would then allow it to derive “Right now, mercury is not at position Y” from “Right now, mercury is not anywhere other than position X”. So while they are not directly contradictory, it is quite easy to see how a direct contradiction could be derived from them, meaning they are indirectly contradictory.

[9] In particular, I suspect that the crossover operation used in the field of genetic programming would be an appropriate method for blindly generating new ideas from old ones, or at least a good starting point for an appropriate method. See John Koza’s book Genetic Programming for details on this operation.

[10] At least, in the most basic version of the theory. It may turn out to be necessary to have some sort of policy that decides what happens when, say, a certain modification does resolve the contradiction, but also leads to some requirement being unmet. Or an even more complex situation, like some modification that resolves a contradiction, but leaves three requirements unfulfilled, while also fulfilling 4 other requirements that were previously unfulfilled. Does there need to be some way of defining which problems and/or requirements are more important than others? This question needs to be explored more, but for now I tentatively guess that the best thing to do is never accept a modification which leaves any requirements unfulfilled.

[11] Since this algorithm takes an unpredictable amount of time to successfully find an acceptable modification, I suspect that a mind would generally work by having several copies of this algorithm running at once in parallel, each possibly focused on solving different problems, along with another parallel process which simply explores the implications of the existing ideas in the idea-set, as is necessary to find new contradictions.

Tags: AGI, Epistemology, CTP Theory